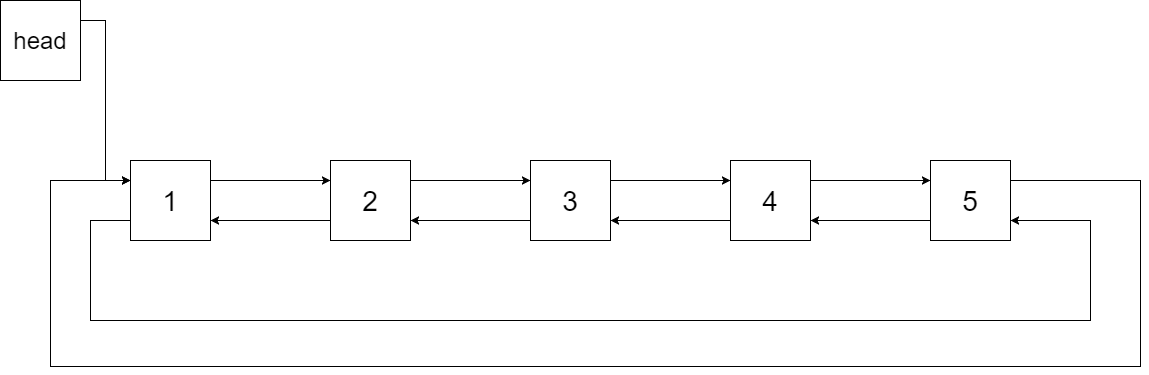
栈 Stack类表示后进先出(LIFO)对象堆栈
1 Stack<Integer> stack = new Stack <>()
Deque
1 Deque<Integer> stack = new ArrayDeque<Integer>();
方法
1 2 3 4 5 6 7 8 9 E peek() 查看此堆栈顶部的对象,而不将其从堆栈中删除。 E pop() 移除此堆栈顶部的对象,并将该对象作为此函数的值返回。 E push (E item) 将项目推到此堆栈的顶部。 isEmpty() a.pop().equals(b) 比较最好用
方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 E peekFirst() 检索但不删除此双端队列的第一个元素,如果此双端队列为空,则返回 null 。 E peekLast() 检索但不删除此双端队列的最后一个元素,如果此双端队列为空,则返回 null 。 void addFirst(E e) 如果可以在不违反容量限制的情况下立即插入指定元素,则在此双端队列的前面插入指定元素,如果当前没有可用空间,则抛出IllegalStateException void addLast(E e) 如果可以在不违反容量限制的情况下立即插入指定元素,则在此双端队列的末尾插入指定元素,如果当前没有可用空间,则抛出IllegalStateException E peekFirst() 检索但不删除此双端队列的第一个元素,如果此双端队列为空,则返回 null 。 E peekLast() 检索但不删除此双端队列的最后一个元素,如果此双端队列为空,则返回 null 。 E removeFirst() 检索并删除此双端队列的第一个元素。 E removeLast() 检索并删除此双端队列的最后一个元素。 int size() 返回此双端队列中的元素数。
一、数据结构和算法-剑指Offer 1.栈与队列 ==有优先考虑,双栈,队列==
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
1 2 3 4 5 6 7 8 9 输入: ["CQueue" ,"appendTail" ,"deleteHead" ,"deleteHead" ] [[],[3 ],[],[]] 输出:[null ,null ,3 ,-1 ] 输入: ["CQueue" ,"deleteHead" ,"appendTail" ,"appendTail" ,"deleteHead" ,"deleteHead" ] [[],[],[5 ],[2 ],[],[]] 输出:[null ,-1 ,null ,null ,5 ,2 ]
解题思路:
利用栈的先入后出的性质,通过两个栈的相互转移颠倒,实现数据的插入和删除功能。
时间复杂度:O(1)
空间复杂度:O(N)
1 2 3 1.定义两个栈 2.第一个栈用来存数据,第二个栈用来存放第一个栈的数据,此时,两个栈的栈顶分别是队列头部和队列尾部。 3.判断栈2是否空,空则判断栈1,栈1空返回-1,不空将栈1放入栈2
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class CQueue { private Stack<Integer> stack1; private Stack<Integer> stack2; public CQueue () { stack1 = new Stack <>(); stack2 = new Stack <>(); } public void appendTail (int value) { stack1.push(value); } public int deleteHead () { if (!stack2.isEmpty()){ return stack2.pop(); }else { while (!stack1.isEmpty()){ stack2.push(stack1.pop()); } return stack2.isEmpty() ? -1 : stack2.pop(); } } }
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
1 2 3 4 5 6 7 8 MinStack minStack = new MinStack ();minStack.push(-2 ); minStack.push(0 ); minStack.push(-3 ); minStack.min(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.min(); --> 返回 -2.
解题思路:
利用辅助栈、即双栈,栈1存储数据,栈2严格遵守最小值规则。
时间复杂度:O(1)
空间复杂度:O(N)
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class MinStack { private Stack<Integer> stack1; private Stack<Integer> stack2; public MinStack () { stack1 = new Stack <>(); stack2 = new Stack <>(); } public void push (int x) { stack1.push(x); if (stack2.empty()||stack2.peek()>=x){ stack2.push(x); } } public void pop () { if (stack1.pop().equals(stack2.peek())){ stack2.pop(); } } public int top () { return stack1.peek(); } public int min () { return stack2.peek(); } }
2.链表 ==考虑辅助栈,队列,递归==
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。 0 <= 链表长度 <= 10000
1 2 输入:head = [1,3,2] 输出:[2,3,1]
解题思路:
一、利用辅助栈,将链表的数据全部取出来放入栈中,利用栈的先入后出原则。
时间复杂度:O(N)
空间复杂度:O(N)
二、原地逆序数组遍历利
时间复杂度:O(N)
空间复杂度:O(N)
三、递归
时间复杂度:O(N)
空间复杂度:O(N)
递归代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { ArrayList<Integer> tem = new ArrayList <>(); public int [] reversePrint(ListNode head) { recur(head); int res[] = new int [tem.size()]; for (int i=0 ;i<res.length;i++){ res[i] = tem.get(i); } return res; } void recur (ListNode head) { if (head==null )return ; recur(head.next); tem.add(head.val); } }
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
1 2 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
解题思路:
一、利用辅助栈,将链表的数据全部取出来放入栈中,利用栈的先入后出原则。
时间复杂度:O(N)
空间复杂度:O(N)
二、迭代
时间复杂度:O(N)
空间复杂度:O(1)
三、递归
时间复杂度:O(N)
空间复杂度:O(N)
迭代代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public ListNode reverseList (ListNode head) { ListNode cur = head ,pure = null ; while (cur!=null ){ ListNode tmp = cur.next; cur.next = pure; pure = cur; cur = tmp; } return pure; } }
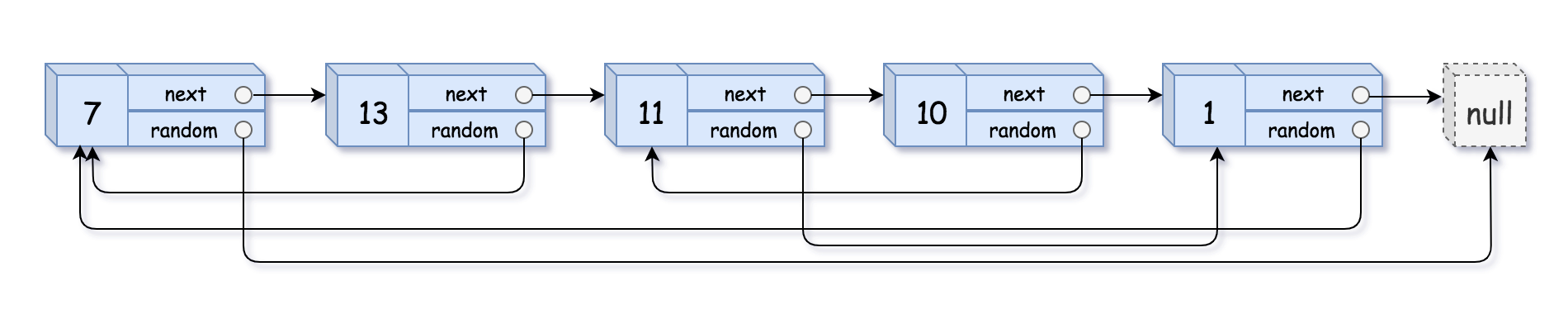
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
1 2 3 4 5 6 7 8 9 10 11 12 输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出:[[7,null],[13,0],[11,4],[10,2],[1,0]] 输入:head = [[1,1],[2,1]] 输出:[[1,1],[2,1]] 输入:head = [[3,null],[3,0],[3,null]] 输出:[[3,null],[3,0],[3,null]] 输入:head = [] 输出:[] 解释:给定的链表为空(空指针),因此返回 null。
解题思路:
该题本质上就是链表的深拷贝
一、利用回溯+哈希表。
时间复杂度:O(n),其中 n 是链表的长度。对于每个节点,我们至多访问其「后继节点」和「随机指针指向的节点」各一次,均摊每个点至多被访问两次。
空间复杂度:O(n),其中 n 是链表的长度。为哈希表的空间开销。
1 其实就是建立一个哈希表,链表的键和值拷贝进去,然后分别读取链表的键,设置值的next和radom指向,最总通过get(head)获取哈希表存放链表的头
二、迭代+拆分
时间复杂度:O(N)
空间复杂度:O(1)
1 2 3 4 把原链表和新链表组合在一起,分别通过.next来访问,注意最后把原链表还原 1.先复制链表,柔和进去 2.设置random链接 3.拆分
方法一代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public Node copyRandomList (Node head) { if (head == null ) return null ; Node cur = head; Map<Node,Node> map = new HashMap <>(); while (cur!=null ){ map.put(cur,new Node (cur.val)); cur = cur.next; } cur = head; while (cur != null ){ map.get(cur).next = map.get(cur.next); map.get(cur).random = map.get(cur.random); cur = cur.next; } return map.get(head); } }
方法二代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution { public Node copyRandomList (Node head) { if (head == null ) return null ; Node cur = head; while (cur!=null ){ Node temp = new Node (cur.val); temp.next = cur.next; cur.next = temp; cur = temp.next; } cur = head; while (cur!=null ){ if (cur.random!=null ){ cur.next.random = cur.random; } cur = cur.next.next; } cur = head.next; Node pre = head , res = head.next; while (cur.next!=null ){ pre.next = pre.next.next; cur.next = cur.next.next; pre = pre.next; cur = res.next; } pre.next = null ; return res; } }
3.字符串 请实现一个函数,把字符串 s 中的每个空格替换成”%20”。
1 2 输入:s = "We are happy." 输出:"We%20are%20happy."
解题思路:
一、数组拷贝。
时间复杂度:O(n)
空间复杂度:O(n)
方法一代码
1 2 3 4 5 6 7 8 9 10 class Solution { public String replaceSpace (String s) { StringBuilder builder = new StringBuilder (); for (Character c : s.toCharArray()) { if (c==' ' )builder.append("%20" ); else builder.append(c); } return builder.toString(); } }
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串”abcdefg”和数字2,该函数将返回左旋转两位得到的结果”cdefgab”。
1 2 3 4 5 输入: s = "abcdefg", k = 2 输出: "cdefgab" 输入: s = "lrloseumgh", k = 6 输出: "umghlrlose"
解题思路:
一、利用String的切片函数。
时间复杂度:O(n)
空间复杂度:O(n)
二、列表遍历拼接。
时间复杂度:O(n)
空间复杂度:O(n)
方法一代码
1 2 3 4 5 class Solution { public String reverseLeftWords (String s, int n) { return new String (s.substring(n)+s.substring(0 ,n)); } }
方法二代码
1 2 3 4 5 6 7 8 9 10 class Solution { public String reverseLeftWords (String s, int n) { StringBuilder res = new StringBuilder (); for (int i = n; i < s.length(); i++) res.append(s.charAt(i)); for (int i = 0 ; i < n; i++) res.append(s.charAt(i)); return res.toString(); } }
4.查找算法二分 找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
1 2 3 输入: [2, 3, 1, 0, 2, 5, 3] 输出:2 或 3
解题思路:
一、利用Set集合。
时间复杂度:O(n)
空间复杂度:O(n)
二、原地交换。
时间复杂度:O(n)
空间复杂度:O(1)
1 2 3 4 5 6 算法流程: 遍历数组 numsnums ,设索引初始值为 i = 0 1.若 nums[i] = i : 说明此数字已在对应索引位置,无需交换,因此跳过; 2.若 nums[nums[i]] = nums[i] : 代表索引 nums[i]处和索引i处的元素值都为nums[i],即找到一组重复值,返回此值 nums[i]; 否则: 交换索引为 i 和 nums[i] 的元素值,将此数字交换至对应索引位置。 若遍历完毕尚未返回,则返回 -1 。
方法一代码
1 2 3 4 5 6 7 8 9 10 11 class Solution { public int findRepeatNumber (int [] nums) { Set<Integer> set = new HashSet <Integer>(); for (int num : nums){ if (!set.add(num)){ return num; } } return -1 ; } }
方法二代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int findRepeatNumber (int [] nums) { int i = 0 ; while (i < nums.length) { if (nums[i] == i) { i++; continue ; } if (nums[nums[i]] == nums[i]) return nums[i]; int tmp = nums[i]; nums[i] = nums[tmp]; nums[tmp] = tmp; } return -1 ; } }
统计一个数字在排序数组中出现的次数。
1 2 3 4 5 6 7 8 9 10 输入: nums = [5,7,7,8,8,10], target = 8 输出: 2 输入: nums = [5,7,7,8,8,10], target = 6 输出: 0 0 <= nums.length <= 105 -109 <= nums[i] <= 109 nums 是一个非递减数组 -109 <= target <= 109
解题思路:
一、利用二分法。
时间复杂度:O(log(N))
空间复杂度:O(1)
1 2 3 4 5 6 7 8 9 10 11 12 1.初始化: 左边界 i = 0,右边界 j = len(nums) - 1 2.循环二分: 当闭区间 [i, j][i,j] 无元素时跳出; 1.计算中点 m = (i + j) / 2m=(i+j)/2 (向下取整); 2.若 nums[m] < target,则 target在闭区间[m+1,j] 中,因此执行 i = m + 1; 3.若 nums[m] > target ,则 target在闭区间 [i,m−1] 中,因此执行 j = m- 1; 4.若 nums[m] = target,则右边界right在闭区间[m+1,j]中;左边界left在闭区间[i,m−1]中,因此分为以下两种情况 1.若查找 右边界right ,则执行 i = m + 1;(跳出时 i 指向右边界) 2.若查找 左边界left ,则执行 j = m - 1;(跳出时 j 指向左边界) 3.返回值: 应用两次二分,分别查找 right 和 left ,最终返回 right - left - 1 即可。 查找完右边界后,可用 nums[j] = j判断数组中是否包含 target,若不包含则直接提前返回 0 ,无需后续查找左边界。 查找完右边界后,左边界 left 一定在闭区间 [0, j] 中,因此直接从此区间开始二分查找即可。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public int search (int [] nums, int target) { int i = 0 , j = nums.length - 1 ; while (i <= j) { int m = (i + j) / 2 ; if (nums[m] <= target) i = m + 1 ; else j = m - 1 ; } int right = i; if (j >= 0 && nums[j] != target) return 0 ; i = 0 ; j = nums.length - 1 ; while (i <= j) { int m = (i + j) / 2 ; if (nums[m] < target) i = m + 1 ; else j = m - 1 ; } int left = j; return right - left - 1 ; } }
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
1 2 3 4 5 6 7 输入: [0,1,3] 输出: 2 输入: [0,1,2,3,4,5,6,7,9] 输出: 8 1 <= 数组长度 <= 10000
解题思路:
一、利用二分法。
时间复杂度:O(n)
空间复杂度:O(1)
1 2 3 4 5 6 1.初始化: 左边界 i = 0,右边界j=len(nums)−1 ;代表闭区间 [i, j] 2.循环二分: 当 i≤j 时循环(即当闭区间 [i,j] 为空时跳出) 1.计算中点 m = (i + j) // 2,其中 "//" 为向下取整除法; 2.若 nums[m] = m,则 “右子数组的首位元素” 一定在闭区间 [m + 1, j]中,因此执行i=m+1, 3.若 nums[m] ≠m ,则 “左子数组的末位元素” 一定在闭区间 [i, m - 1]中,因此执行 j = m - 1; 3.返回值:跳出时,变量 i 和 j 分别指向 “右子数组的首位元素” 和 “左子数组的末位元素” 。因此返回 i 即可。
代码
1 2 3 4 5 6 7 8 9 10 11 class Solution { public int missingNumber (int [] nums) { int i = 0 , j = len(nums) - 1 ; while (i<=j){ int m = (i+j)/2 ; if (nums[m]==m)i=m+1 ; else j = m-1 ; } return i; } }
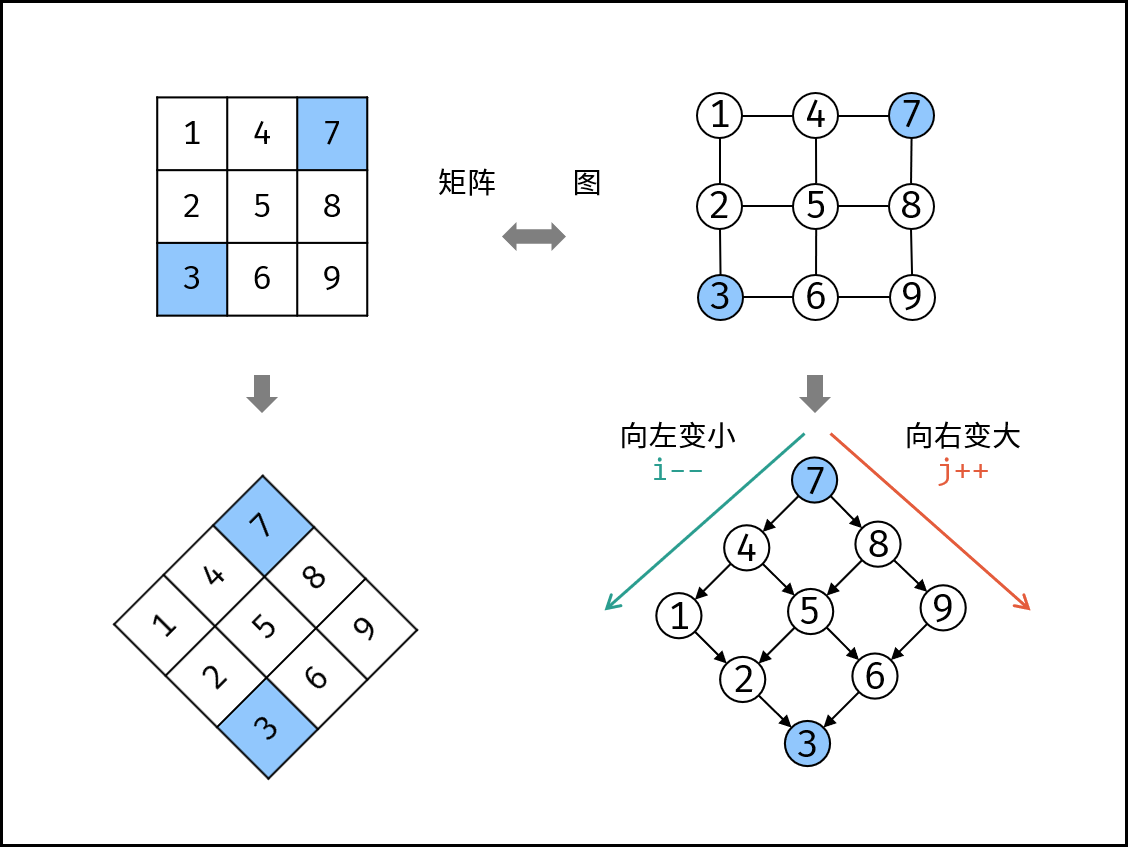
5.查找算法 在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 现有矩阵 matrix 如下: [ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ] 给定 target = 5,返回 true。 给定 target = 20,返回 false 限制: 0 <= n <= 1000 0 <= m <= 1000
解题思路:
一、利用二分法,可类似成二叉树,将矩阵旋转,。
时间复杂度:O(n)
空间复杂度:O(1)
1 2 3 4 从矩阵 matrix 左下角元素(索引设为 (i, j) )开始遍历,并与目标值对比: 当 matrix[i][j] > target 时,执行 i-- ,即消去第 i 行元素; 当 matrix[i][j] < target 时,执行 j++ ,即消去第 j 列元素; 当 matrix[i][j] = target 时,返回 truetrue ,代表找到目标值。
代码
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public boolean findNumberIn2DArray (int [][] matrix, int target) { int i = matrix.length - 1 , j = 0 ; while (i >= 0 && j < matrix[0 ].length) { if (matrix[i][j] > target) i--; else if (matrix[i][j] < target) j++; else return true ; } return false ; } }
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为1。
1 2 3 4 5 输入:[3,4,5,1,2] 输出:1 输入:[2,2,2,0,1] 输出:0
解题思路:
一、利用二分法
时间复杂度:O(log(N))
空间复杂度:O(1)
1 2 3 4 5 6 1.初始化,i=0,j=numbers.length-1; 2.循环查找 m=(i+j)/2 i<=m<j 1.如果munbers[m]<number[j],则该数一定在左边,令j=m; 2.如果munbers[m]>number[j],则该数一定在右边,令i=m+1; 3.如果munbers[m]=number[j],则该数不一定,j=j-1; 3.返回值: 当 i = j 时跳出二分循环,并返回 旋转点的值 nums[i] 即可
代码
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int minArray (int [] numbers) { int i=0 ,j=numbers.length-1 ; while (i!=j){ int m = (i+j)/2 ; if (numbers[m]<numbers[j])j=m; else if (numbers[m]>numbers[j])i=m+1 ; else j=j-1 ; } return numbers[i]; } }
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印
1 2 3 4 5 6 7 8 给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回:[3,9,20,15,7]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public int [] levelOrder(TreeNode root) { if (root==null )return new int [0 ]; Queue<TreeNode> queue = new LinkedList <>(); queue.add(root); ArrayList<Integer> ans = new ArrayList <>(); while (!queue.isEmpty()){ TreeNode node = queue.poll(); ans.add(node.val); if (node.left!=null ) queue.add(node.left); if (node.right!=null ) queue.add(node.right); } int [] res = new int [ans.size()]; for (int i=0 ;i<ans.size();i++){ res[i] = ans.get(i); } return res; } }
6.搜索与回溯算法(广度优先搜索) 广度优先搜索算法(Breadth-First Search,缩写为 BFS),又称为宽度优先搜索,是一种图形搜索算法。简单的说,BFS 是从根结点开始,沿着树的宽度遍历树的结点。如果所有结点均被访问,则算法中止。
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 例如: 给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回其层次遍历结果: [ [3], [9,20], [15,7] ]
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public List<List<Integer>> levelOrder (TreeNode root) { Queue<TreeNode> queue = new LinkedList <>(); if (root != null ) queue.add(root); List<List<Integer>> ans = new ArrayList <>(); while (!queue.isEmpty()){ ArrayList<Integer> arry = new ArrayList <>(); for (int i = queue.size();i>0 ;i--){ TreeNode node = queue.poll(); arry.add(node.val); if (node.left!=null ) queue.add(node.left); if (node.right!=null ) queue.add(node.right); } ans.add(arry); } return ans; } }
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
1 2 3 4 5 6 7 8 9 10 11 12 13 例如: 给定二叉树: [3,9,20,null,null,15,7] 3 / \ 9 20 / \ 15 7 返回其层次遍历结果: [ [3], [20,9], [15,7] ]
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public List<List<Integer>> levelOrder (TreeNode root) { Queue<TreeNode> queue = new LinkedList <>(); if (root != null ) queue.add(root); List<List<Integer>> ans = new ArrayList <>(); while (!queue.isEmpty()){ LinkedList<Integer> arry = new LinkedList <>(); for (int i = queue.size();i>0 ;i--){ TreeNode node = queue.poll(); if (ans.size() % 2 ==0 )arry.addLast(node.val); else arry.addFirst(node.val); if (node.left!=null ) queue.add(node.left); if (node.right!=null ) queue.add(node.right); } ans.add(arry); } return ans; } }
7.搜索与回溯算法(深度优先搜索) 深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构) B是A的子结构, 即 A中有出现和B相同的结构和节点值。 例如: 给定的树 A: 3 / \ 4 5 / \ 1 2 给定的树 B: 4 / 1 返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。 示例 1: 输入:A = [1,2,3], B = [3,1] 输出:false 示例 2: 输入:A = [3,4,5,1,2], B = [4,1] 输出:true
解题思路:
一、先序遍历 + 包含判断
时间复杂度:O(MN)
空间复杂度:O(M)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 若树B是树A的子结构,则子结构的根节点可能为树A的任意一个节点.因此,判断树B是否是树A的子结构,需完成以下两步工作: 1.先序遍历树 A 中的每个节点 n(a) (对应函数 isSubStructure(A, B)) 2.判断树 A 中 以 n(a) 为根节点的子树是否包含树 B (对应函数 recur(A, B)) recur(A, B) 函数: 1.终止条件: 1.当节点 B 为空:说明树 B 已匹配完成(越过叶子节点),因此返回 true ; 2.当节点 A 为空:说明已经越过树 A 叶子节点,即匹配失败,返回 false ; 3.当节点 A 和 B 的值不同:说明匹配失败,返回 false ; 2.返回值: 判断 A 和 B 的左子节点是否相等,即 recur(A.left, B.left) ; 判断 A 和 B 的右子节点是否相等,即 recur(A.right, B.right) ; isSubStructure(A, B) 函数: 特例处理: 当树 A 为空或树 B 为空时,直接返回 false ; 返回值: 若树 B 是树 A 的子结构,则必满足以下三种情况之一,因此用或 || 连接; 1.以节点 A 为根节点的子树 包含树 B ,对应 recur(A, B); 2.树 B 是树 A 左子树的子结构,对应 isSubStructure(A.left, B); 3.树 B 是树 A 右子树的子结构,对应 isSubStructure(A.right, B);
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public boolean isSubStructure (TreeNode A, TreeNode B) { return (A!=null &&B!=null ) && ( recur(A, B)||isSubStructure(A.left, B)||isSubStructure(A.right, B) ) } boolean recur (TreeNode A, TreeNode B) { if (B==null ) return true ; if (A==null || A.val != B.val) return false ; return recur(A.left, B.left)&&recur(A.right, B.right); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 请完成一个函数,输入一个二叉树,该函数输出它的镜像。 例如输入: 4 / \ 2 7 / \ / \ 1 3 6 9 镜像输出: 4 / \ 7 2 / \ / \ 9 6 3 1 输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1] 0 <= 节点个数 <= 1000
解题思路:
一、递归法
根据二叉树镜像的定义,考虑递归遍历(dfs)二叉树,交换每个节点的左 / 右子节点,即可生成二叉树的镜像。
1 2 3 4 5 6 1.终止条件: 当节点 root 为空时(即越过叶节点),则返回 null ; 2.递推工作: 1.初始化节点 tmp ,用于暂存 root 的左子节点; 2.开启递归 右子节点 mirrorTree(root.right),并将返回值作为 root 的左子节点 3.开启递归 左子节点 mirrorTree(tmp),并将返回值作为 root 的右子节点 3.返回值:返回当前节点 root
二、辅助栈(或队列)
利用栈(或队列)遍历树的所有节点 nodenode ,并交换每个 nodenode 的左 / 右子节点。
1 2 3 4 5 6 7 1.特例处理: 当 root 为空时,直接返回 null ; 2.初始化: 栈(或队列),本文用栈,并加入根节点 root 。 3.循环交换: 当栈 stack 为空时跳出; 1.出栈: 记为 node ; 2.添加子节点: 将 node 左和右子节点入栈; 3.交换: 交换 node 的左 / 右子节点。 4.返回值: 返回根节点 root 。
方法一递归代码
1 2 3 4 5 6 7 8 9 class Solution { public TreeNode mirrorTree (TreeNode root) { if (root == null ) return null ; TreeNode tmp = root.left; root.left = mirrorTree(root.right); root.right = mirrorTree(tmp); return root; } }
方法二栈代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public TreeNode mirrorTree (TreeNode root) { if (root == null ) return null ; Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); if (node.left!=null )stack.add(node.left); if (node.right!=null )stack.add(node.right); TreeNode temp = node.left; node.left = node.right; node.right = temp; } return root; } }
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 1 / \ 2 2 / \ / \ 3 4 4 3 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的: 1 / \ 2 2 \ \ 3 3 示例 1: 输入:root = [1,2,2,3,4,4,3] 输出:true 示例 2: 输入:root = [1,2,2,null,3,null,3] 输出:false
解题思路:
一、递归法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 对称二叉树定义: 对于树中任意两个对称节点LL和RR,一定有: L.val = R.val :即此两对称节点值相等。 L.left.val = R.right.val :即 L 的 左子节点 和 R 的 右子节点 对称; L.right.val = R.left.val:即 L 的 右子节点 和 R 的 左子节点 对称。 根据以上规律,考虑从顶至底递归,判断每对节点是否对称,从而判断树是否为对称二叉树。 isSymmetric(root) 特例处理: 若根节点 root 为空,则直接返回 true。 返回值: 即 recur(root.left, root.right) ; recur(L, R) 终止条件: 当 L 和 R 同时越过叶节点: 此树从顶至底的节点都对称,因此返回 true ; 当 L 或 R 中只有一个越过叶节点: 此树不对称,因此返回 false ; 当节点 L ≠ 节点 R 值: 此树不对称,因此返回 false ; 递推工作: 判断两节点 L.left 和 R.right 是否对称,即 recur(L.left, R.right) ; 判断两节点 L.right 和 R.left 是否对称,即 recur(L.right, R.left) ; 返回值: 两对节点都对称时,才是对称树,因此用与逻辑符 && 连接。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public boolean isSymmetric (TreeNode root) { return root = = null ? true : recur(root.left, root.right); } boolean recur (TreeNode left,TreeNode right) { if (left==null &&right==null )return true ; if (left==null ||right==null ||left.val!=right.val)return false ; return recur(L.left, R.right)&&recur(L.right, R.left); } }
8.动态规划 1.简单 动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
1 2 3 4 5 F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。 答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
方法一:动态规划
1 2 3 4 5 斐波那契数的边界条件是 F(0)=0 和 F(1)=1。当 n>1 时,每一项的和都等于前两项的和,因此有如下递推关系: F(n)=F(n-1)+F(n-2) 由于斐波那契数存在递推关系,因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系,边界条件为 F(0) 和 F(1)。 根据状态转移方程和边界条件,可以得到时间复杂度和空间复杂度都是O(n) 的实现。由于 F(n) 只和 F(n−1) 与F(n−2) 有关,因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)。如下的代码中给出的就是这种实现。
方法二:递归
1 2 原理: 把 f(n)问题的计算拆分成 f(n-1) 和 f(n-2)两个子问题的计算,并递归,以 f(0) 和 f(1) 为终止条件。 缺点: 大量重复的递归计算,例如 f(n) 和 f(n - 1)两者向下递归需要 各自计算 f(n - 2)的值。
方法三:矩阵快速幂
方法一代码
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int fib (int n) { final int MOD = 1000000007 ; if (n<2 )return n; int r = 1 , p = 0 , q = 0 ; for (int i = 2 ;i<=n;i++){ p = q; q = r; r=(p+q)%MOD; } return r; } }
方法三代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { static final int MOD = 1000000007 ; public int fib (int n) { if (n < 2 ) { return n; } int [][] q = {{1 , 1 }, {1 , 0 }}; int [][] res = pow(q, n - 1 ); return res[0 ][0 ]; } public int [][] pow(int [][] a, int n) { int [][] ret = {{1 , 0 }, {0 , 1 }}; while (n > 0 ) { if ((n & 1 ) == 1 ) { ret = multiply(ret, a); } n >>= 1 ; a = multiply(a, a); } return ret; } public int [][] multiply(int [][] a, int [][] b) { int [][] c = new int [2 ][2 ]; for (int i = 0 ; i < 2 ; i++) { for (int j = 0 ; j < 2 ; j++) { c[i][j] = (int ) (((long ) a[i][0 ] * b[0 ][j] + (long ) a[i][1 ] * b[1 ][j]) % MOD); } } return c; } }
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。问题同上一题
1 2 3 4 5 6 7 8 输入:n = 2 输出:2 输入:n = 7 输出:21 输入:n = 0 输出:1
方法一 矩阵快速幂
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution { static final int MOD = 1000000007 ; public int numWays (int n) { if (n < 2 ) { return 1 ; } int [][] q = {{1 , 1 }, {1 , 0 }}; int [][] res = curr(q, n ); return res[0 ][0 ]; } public int [][] curr(int [][] a, int n){ int [][] dir = {{1 ,0 },{0 ,1 }}; while (n>0 ){ if ((n&1 )==1 )dir =mutiply(a,dir); a = mutiply(a,a); n>>=1 ; } return dir; } public int [][] mutiply(int [][] a,int [][] b){ int [][] tem = new int [2 ][2 ]; for (int i=0 ;i<2 ;i++){ for (int j=0 ;j<2 ;j++){ tem[i][j]=(int )(((long )a[i][0 ]*b[0 ][j]+(long )a[i][1 ]*b[1 ][j])%MOD); } } return tem; } }
方法二 动态规划
1 2 3 4 5 6 7 8 9 10 11 class Solution { public int numWays (int n) { int a = 1 , b = 1 , sum; for (int i = 0 ; i < n; i++){ sum = (a + b) % 1000000007 ; a = b; b = sum; } return a; } }
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
1 2 3 4 5 6 7 8 输入: [7,1,5,3,6,4] 输出: 5 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。 输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
方法一:暴力法
方法二:动态规划
1 2 3 4 5 6 7 8 9 10 11 class Solution { public int maxProfit (int [] prices) { int minprice = Integer.MAX_VALUE; int pro = 0 ; for (int price:prices){ if (minprice>price)minprice = price; else if (minprice<price)pro = Math.max(pro,price-minprice); } return pro; } }
2.中等 输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
1 2 3 输入: nums = [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
方法一、动态规划
方法二、暴力
常见解法
时间复杂度
空间复杂度
暴力搜索
O(N^2)
O(1)
分治思想
O(NlogN)
O(logN)
动态规划
O (N )O(1)
方法三、分治思想
1 2 3 4 5 6 7 8 9 10 class Solution { public int maxSubArray (int [] nums) { int res=nums[0 ]; for (int i=1 ;i<nums.length;i++){ nums[i] += Math.max(nums[i-1 ],0 ); res = Math.max(res,nums[i]); } return res; } }
礼物的最大价值
9.双指针(简单) 给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
1 2 3 4 5 6 7 输入: head = [4,5,1,9], val = 5 输出: [4,1,9] 解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9. 输入: head = [4,5,1,9], val = 1 输出: [4,5,9] 解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.
解题思路:
一、顺序查找,直接遍历
时间复杂度:O(N)
空间复杂度:O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { public ListNode deleteNode (ListNode head, int val) { if (head.val==val)return head.next; ListNode pre = head,node = head.next; while ( node != null && node.val != val){ pre = node; node = node.next; } if (node!=null )pre.next = node.next; return head; } }
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
1 2 3 给定一个链表: 1->2->3->4->5, 和 k = 2. 返回链表 4->5.
解题思路:
一、直接遍历
二、双指针遍历(快慢指针)
快慢指针的思想。我们将第一个指针 fast 指向链表的第 k + 1个节点,第二个指针 slow 指向链表的第一个节点,此时指针 fast 与 slow 二者之间刚好间隔 k 个节点。此时两个指针同步向后走,当第一个指针fast 走到链表的尾部空节点时,则此时slow 指针刚好指向链表的倒数第k个节点。
一、直接遍历代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { public ListNode getKthFromEnd (ListNode head, int k) { int n=0 ; ListNode node=head; for (;node != null ;node = node.next)n++; node=head; for (int i = 0 ;i<n-k;i++){ node = node.next; } return node; } }
二、双指针遍历(快慢指针)代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public ListNode getKthFromEnd (ListNode head, int k) { ListNode fast = head,slow = head; for (k>0 ;k++)fast = fast.next; while (fast!=null ){ slow=slow.next;fast=fast.next; } return slow; } }
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
示例1:
1 2 3 4 输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4 0 <= 链表长度 <= 1000
方法一、顺序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public ListNode mergeTwoLists (ListNode l1, ListNode l2) { if (l1==null )return l2; if (l2==null )return l1; ListNode node = new ListNode (0 ); ListNode head = node; while (l1!=null &&l2!=null ){ if (l1.val<l2.val){ node.next = l1; l1 = l1.next; }else { node.next = l2; l2 = l2.next; } node = node.next; } if (l1 == null ) node.next = l2; if (l2 == null ) node.next = l1; return head.next; } }
方法二、递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public ListNode mergeTwoLists (ListNode l1, ListNode l2) { if (l1 ==null ) return l2; if (l2 ==null ) return l1; if (l1.val<l2.val){ l1.next = mergeTwoLists(l1.next,l2); return l1; }else { l2.next = mergeTwoLists(l1,l2.next); return l2; } } }
输入两个链表,找出它们的第一个公共节点。
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
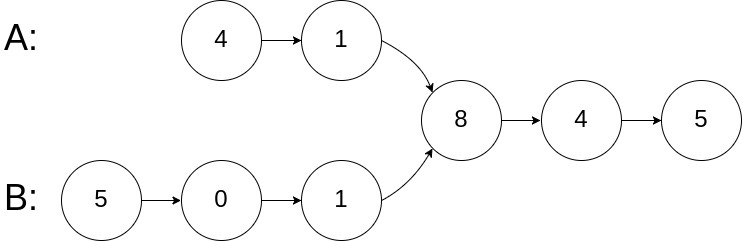
1 2 3 输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Reference of the node with value = 8 输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
1 2 3 输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Reference of the node with value = 2 输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
1 2 3 4 输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 解释:这两个链表不相交,因此返回 null。
1 2 3 4 如果两个链表没有交点,返回 null. 在返回结果后,两个链表仍须保持原有的结构。 可假定整个链表结构中没有循环。 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
方法一、双指针
O(n+m) 时间复杂度,空间 O(m)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public class Solution { public ListNode getIntersectionNode (ListNode headA, ListNode headB) { if (headA == null || headB == null )return null ; ListNode pA = headA,pB = headB; while (pA!=pB){ pA = pA==null ? headB : pA.next; pB = pB==null ? headA : pB.next; } return pA; } }
方法二、哈希集合
O(n+m) 时间复杂度,空间 O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public class Solution { public ListNode getIntersectionNode (ListNode headA, ListNode headB) { Set<ListNode> visited = new HashSet <ListNode>(); ListNode temp = headA; while (temp != null ) { visited.add(temp); temp = temp.next; } temp = headB; while (temp != null ) { if (visited.contains(temp)) { return temp; } temp = temp.next; } return null ; } }
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数在数组的前半部分,所有偶数在数组的后半部分。
1 2 3 4 5 6 7 输入:nums = [1,2,3,4] 输出:[1,3,2,4] 注:[3,1,2,4] 也是正确的答案之一。 0 <= nums.length <= 50000 0 <= nums[i] <= 10000
方法一、双指针
O(n) 时间复杂度,空间 O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int [] exchange(int [] nums) { int left = 0 , right = nums.length - 1 ; while (left<right){ if (nums[left]%2 ==1 )left++; if (nums[right]%2 ==0 )right--; if (nums[left]%2 ==0 && nums[right]%2 ==1 && left<right){ int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; } } return nums; } }
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
1 2 3 4 5 6 7 8 输入:nums = [2,7,11,15], target = 9 输出:[2,7] 或者 [7,2] 输入:nums = [10,26,30,31,47,60], target = 40 输出:[10,30] 或者 [30,10] 1 <= nums.length <= 10^5 1 <= nums[i] <= 10^6
方法一、双指针
O(n) 时间复杂度,空间 O(1)
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int [] twoSum(int [] nums, int target) { int right = nums.length-1 , left = 0 ; while (nums[right]>target)right--; while (left<right){ if (nums[left]+nums[right]>target)right--; else if (nums[left]+nums[right]<target) left++; else return new int [] {nums[left],nums[right]}; } return new int [0 ]; } }
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串”I am a student. “,则输出”student. a am I”。
1 2 3 4 5 6 7 8 9 10 输入: "the sky is blue" 输出: "blue is sky the" 输入: " hello world! " 输出: "world! hello" 解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。 输入: "a good example" 输出: "example good a" 解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
方法一、双指针
O(n) 时间复杂度,空间 O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public String reverseWords (String s) { s = s.trim(); StringBuilder res = new StringBuilder (); int left = s.length-1 ; right = left; while (left>0 ){ while (s.charAt(left)!=' ' )left--; res.append( s.substring(left+1 ,right) + " " ); while (s.charAt(right)!=' ' )left--; right = left; } return res.toString(); } } public String substring (int beginIndex, int endIndex) 返回一个字符串,该字符串是此字符串的子字符串。 子字符串从指定的beginIndex开始,并扩展到索引endIndex - 1 处的字符。 因此子串的长度是endIndex-beginIndex 。
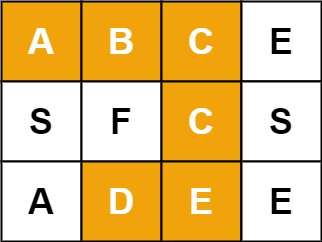
10.搜索与回溯算法(中等) 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 “ABCCED”(单词中的字母已标出)。
1 2 3 4 5 6 7 8 9 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true 输入:board = [["a","b"],["c","d"]], word = "abcd" 输出:false 1 <= board.length <= 200 1 <= board[i].length <= 200 board 和 word 仅由大小写英文字母组成
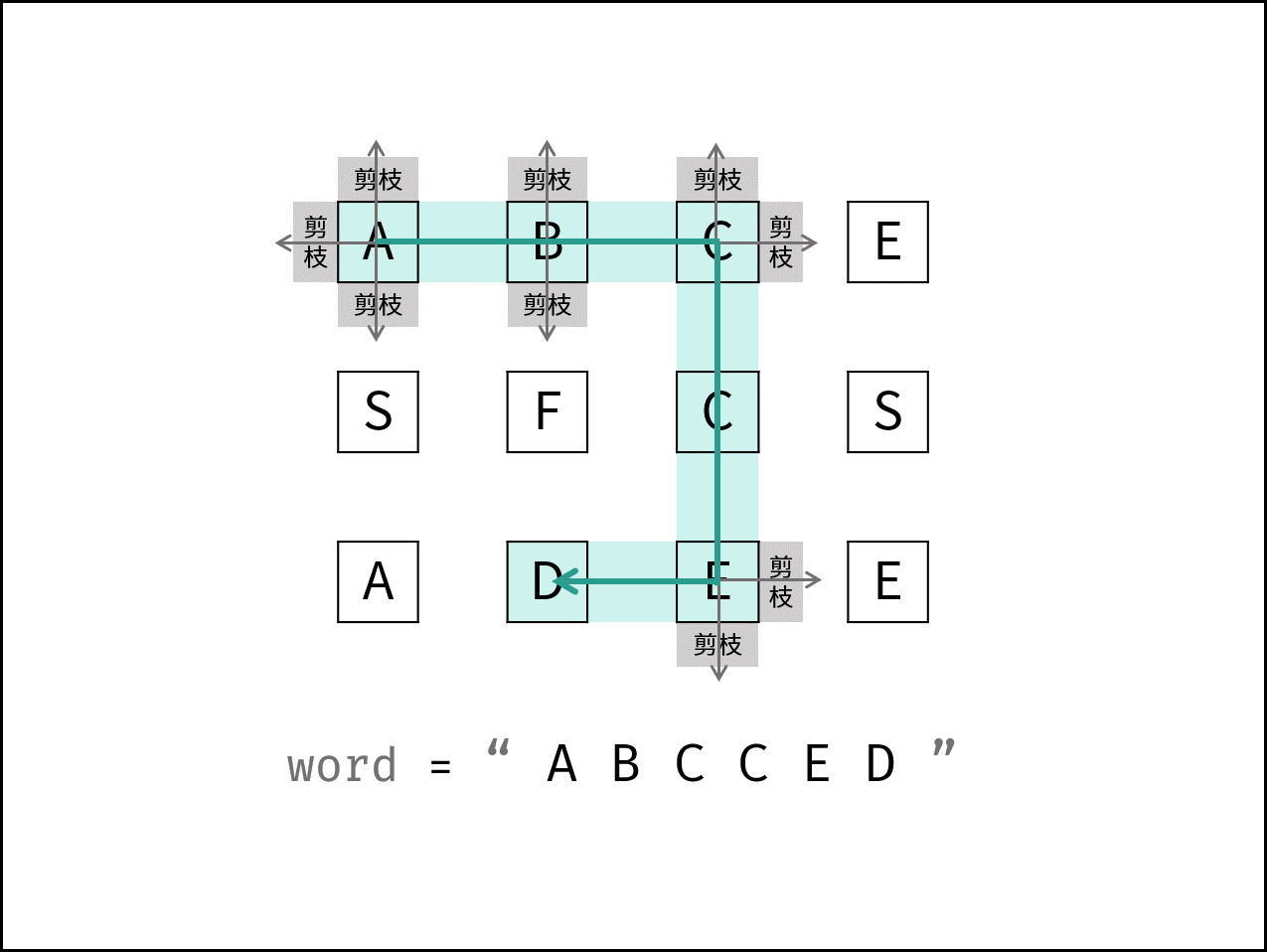
方法一、深度优先搜索DFS+剪枝
深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推。
DFS 解析:
1.递归参数:
1 当前元素在矩阵 board 中的行列索引 i 和 j ,当前目标字符在 word 中的索引 k 。
2.终止条件:
1 2 3 1.返回 falsefalse : (1) 行或列索引越界 或 (2) 当前矩阵元素与目标字符不同 或 (3) 当前矩阵元素已访问过 ( (3) 可合并至 (2) ) 2.返回 truetrue : k = len(word) - 1 ,即字符串 word 已全部匹配。
递推工作:
1 2 3 1.标记当前矩阵元素: 将 board[i][j] 修改为 空字符 '' ,代表此元素已访问过,防止之后搜索时重复访问。 2.搜索下一单元格: 朝当前元素的 上、下、左、右 四个方向开启下层递归,使用 或 连接 (代表只需找到一条可行路径就直接返回,不再做后续 DFS ),并记录结果至 res 。 3.还原当前矩阵元素: 将 board[i][j] 元素还原至初始值,即 word[k] 。
返回值:
1 2 返回布尔量 res ,代表是否搜索到目标字符串。
使用空字符(Python: ‘’ , Java/C++: ‘\0’ )做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时,此算法会将矩阵原有字符认作标记字符,从而出现错误。
1 2 3 4 5 6 时间复杂度 O(3 ^K MN): 最差情况下,需要遍历矩阵中长度为 K 字符串的所有方案,时间复杂度为 O(3 ^K) );矩阵中共有 MN 个起点,时间复杂度为 O(MN) 。 方案数计算: 设字符串长度为 K ,搜索中每个字符有上、下、左、右四个方向可以选择,舍弃回头(上个字符)的方向,剩下 3 种选择,因此方案数的复杂度为 O(3 ^K) 。 空间复杂度 O(K) : 搜索过程中的递归深度不超过 K ,因此系统因函数调用累计使用的栈空间占用 O(K) (因为函数返回后,系统调用的栈空间会释放)。最坏情况下 K=MN ,递归深度为 MN ,此时系统栈使用 O(MN) 的额外空间。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { public boolean exist (char [][] board, String word) { char [] wordarry = word.toCharArray(); for (int i=0 ;i<board.length;i++) for (int j=0 ;j<board[0 ].length;j++){ if ( cur(board,wordarry,i,j,0 ))return true ; } return false ; } boolean cur (char [][] board,char [] wordarry,int i,int j,int k) { if (i<0 ||i>=board.length||j<0 ||j>=board[0 ].length||board[i][j]!=wordarry[k])return false ; if (k == wordarry.length - 1 )return true ; board[i][j] = '\0' ; boolean res = cur(board,wordarry,i+1 ,j,k+1 )||cur(board,wordarry,i,j+1 ,k+1 )||cur(board,wordarry,i-1 ,j,k+1 )||cur(board,wordarry,i,j-1 ,k+1 ); board[i][j] = wordarry[k]; return res; } }
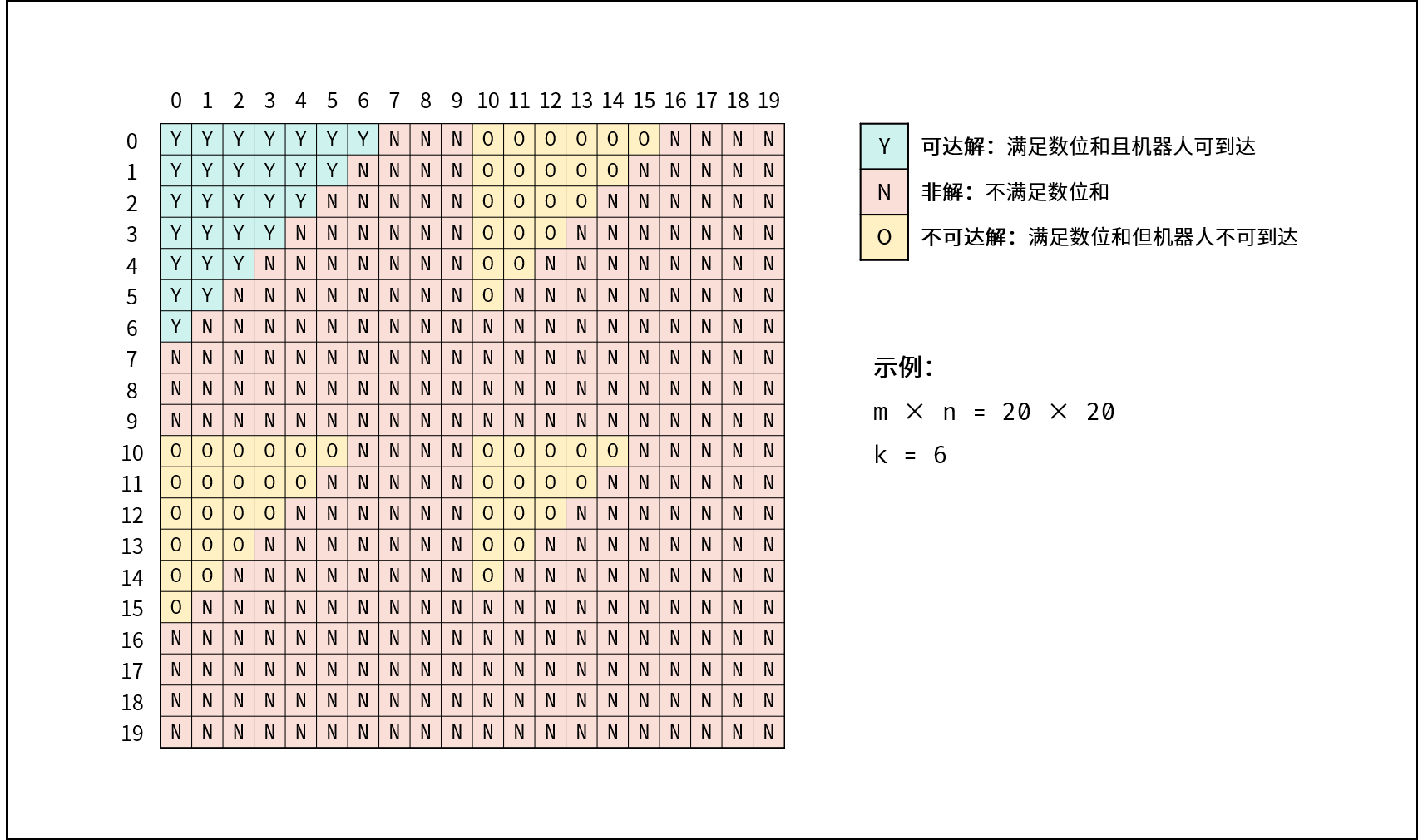
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
1 2 3 4 5 6 7 8 输入:m = 2, n = 3, k = 1 输出:3 输入:m = 3, n = 1, k = 0 输出:1 1 <= n,m <= 100 0 <= k <= 20
方法一、深度优先搜索
算法解析:
递归参数:
1 当前元素在矩阵中的行列索引 i 和 j ,两者的数位和 si, sj 。
**终止条件:
1 当 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过 时,返回 00 ,代表不计入可达解。
递推工作:
1 2 3 4 标记当前单元格 :将索引 (i, j) 存入 Set visited 中,代表此单元格已被访问过。 搜索下一单元格: 计算当前元素的 下、右 两个方向元素的数位和,并开启下层递归 。 回溯返回值: 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数,代表从本单元格递归搜索的可达解总数。
回溯返回值:
1 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数,代表从本单元格递归搜索的可达解总数。
递归代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { int m,n,k; boolean [][] visited; public int movingCount (int m, int n, int k) { this .m = m; this .n = n; this .k = k; this .visited = new boolean [m][n]; return dfs(0 ,0 ,0 ,0 ); } int dfs (int i,int j,int si,int sj) { if (i>=m||j>=n||si+sj>k||visited[i][j])return 0 ; visited[i][j] = true ; return 1 + dfs(i+1 ,j,(i+1 )%10 ==0 ? si-8 : si+1 ,sj) + dfs(i,j+1 ,si,(j+1 )%10 ==0 ? sj-8 : sj+1 ); } }
方法二、广度优先搜索BFS
BFS/DFS : 两者目标都是遍历整个矩阵,不同点在于搜索顺序不同。DFS 是朝一个方向走到底,再回退,以此类推;BFS 则是按照“平推”的方式向前搜索。
**BFS 实现: **通常利用队列实现广度优先遍历。
初始化:
1 将机器人初始点 (0, 0) 加入队列 queue ;
迭代终止条件:
迭代工作:
1 2 3 4 单元格出队: 将队首单元格的 索引、数位和 弹出,作为当前搜索单元格。 判断是否跳过: 若 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过 时,执行 continue 。 标记当前单元格 :将单元格索引 (i, j) 存入 Set visited 中,代表此单元格 已被访问过 。 单元格入队: 将当前元素的 下方、右方 单元格的 索引、数位和 加入 queue 。
返回值:
1 Set visited 的长度 len(visited) ,即可达解的数量。
广度优先搜索BFS代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public int movingCount (int m, int n, int k) { boolean [][] visited = new boolean [m][n]; int res = 0 ; Queue<int []> queue = new LinkedList <int []>(); queue.add(new int []{0 ,0 ,0 ,0 }); while (queue.size()>0 ){ int [] temp = queue.poll(); int i = temp[0 ],j=temp[1 ],si=temp[2 ],sj=temp[3 ]; if (i>=m||j>=n||si+sj>k||visited[i][j])continue ; visited[i][j] = true ; res++; queue.add(new int []{temp[0 ]+1 ,temp[1 ],(temp[0 ]+1 )%10 ==0 ? temp[2 ]-8 : temp[2 ]+1 ,temp[3 ]}); queue.add(new int []{temp[0 ],temp[1 ]+1 ,temp[2 ],(temp[1 ]+1 )%10 ==0 ? temp[3 ]-8 : temp[3 ]+1 }); } return res; } }
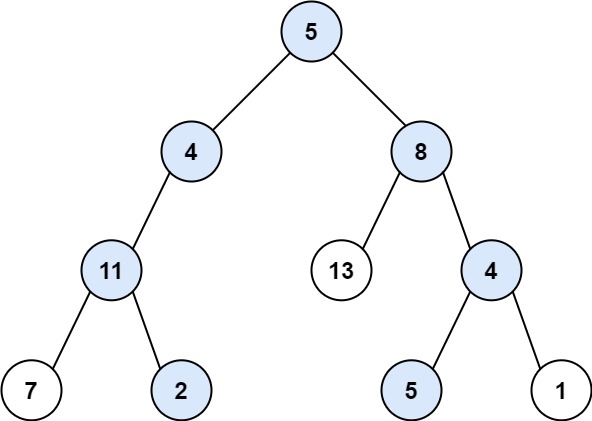
给你二叉树的根节点 root 和一个整数目标和 targetSum , 找出所有从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
1 2 输入:root = [1,2,3], targetSum = 5 输出:[]
1 2 输入:root = [1,2], targetSum = 0 输出:[]
1 2 3 树中节点总数在范围 [0, 5000] 内 -1000 <= Node.val <= 1000 -1000 <= targetSum <= 1000
方法一、深度优先搜索DFS
算法解析:
递归参数:
1 2 3 4 List<List<Integer>> 存放所有的结果 队列存放路线 当前节点的子节点 target剩余的值
**终止条件:
1 2 当节点为空,立即返回 target==0 并且没有子节点,表明搜索到了。将该队列路线加入list
递推工作:
1 2 3 将当前值入队列,路线 左孩子和右孩子放入递归中, 说明路线不通或者已经走通,将当前加入队列的值删掉
回溯返回值:
递归代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { List<List<Integer>> ret = new LinkedList <List<Integer>>(); Deque<Integer> path = new LinkedList <Integer>(); public List<List<Integer>> pathSum (TreeNode root, int target) { dfs(root, target); return ret; } public void dfs (TreeNode root, int target) { if (root == null ) { return ; } path.offerLast(root.val); target -= root.val; if (root.left == null && root.right == null && target == 0 ) { ret.add(new LinkedList <Integer>(path)); } dfs(root.left, target); dfs(root.right, target); path.pollLast(); } }
方法二、广度优先搜索BFS
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
方法一、深度优先搜索DFS
算法流程:
dfs(cur): 递归法中序遍历;
1.终止条件:
1 当节点 cur 为空,代表越过叶节点,直接返回;
2.递归左子树 ,
3.构建链表:
1 2 3 1.当 pre 为空时: 代表正在访问链表头节点,记为 head ; 2.当 pre 不为空时: 修改双向节点引用,即 pre.right = cur , cur.left = pre ; 3.保存 cur : 更新 pre = cur ,即节点 cur 是后继节点的 pre ;
4.递归右子树
treeToDoublyList(root):
1.特例处理: 若节点 root 为空,则直接返回;
2.初始化: 空节点 pre ;
3.转化为双向链表: 调用 dfs(root) ;
4.构建循环链表: 中序遍历完成后,head 指向头节点, pre 指向尾节点,因此修改 head 和 pre 的双向节点引用即可;
5.返回值: 返回链表的头节点 head 即可;
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { Node pre,head; public Node treeToDoublyList (Node root) { if (root == null ) return null ; dfs(root); head.left = pre; pre.right = head; return head; } void dfs (Node cur) { if (cur == null )return ; dfs(cur.left); if (pre == null )head = cur; else {pre.right = cur; } cur.left = pre; pre = cur; dfs(cur.right); } }
给定一棵二叉搜索树,请找出其中第 k 大的节点的值。
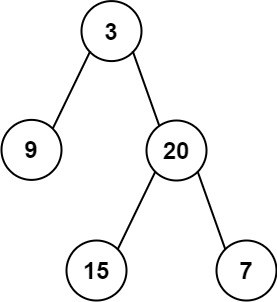
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 输入: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 输出: 4 输入: root = [5,3,6,2,4,null,null,1], k = 3 5 / \ 3 6 / \ 2 4 / 1 输出: 4 1 ≤ k ≤ 二叉搜索树元素个数
方法一、深度优先搜索DFS
算法流程:
1.终止条件:
1 当节点 cur 为空,代表越过叶节点,反回, 如果K==0;找到第k大数返回。
2.递归右子树 ,
3.递归:
4.递归左子树
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { int k,aim; public int kthLargest (TreeNode root, int k) { this .k = k; dfs(root); return aim; } void dfs (TreeNode root) { if (root == null )return ; dfs(root.right); if (k == 0 ) return ; if (--k == 0 )aim = root.val; dfs(root.left); } }
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
返回它的最大深度 3 。
方法一、深度优先搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { int cnt = 0 ; public int maxDepth (TreeNode root) { if (root == null )return 0 ; return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1 ; } }
方法二、广度优先搜索BFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int maxDepth (TreeNode root) { if (root == null ) return 0 ; List<TreeNode> queue = new LinkedList <>() {{ add(root); }}, tmp; int res = 0 ; while (!queue.isEmpty()) { tmp = new LinkedList <>(); for (TreeNode node : queue) { if (node.left != null ) tmp.add(node.left); if (node.right != null ) tmp.add(node.right); } queue = tmp; res++; } return res; } }
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
给定二叉树 [3,9,20,null,null,15,7]
1 2 3 4 5 6 3 / \ 9 20 / \ 15 7 返回 true
给定二叉树 [1,2,2,3,3,null,null,4,4]
1 2 3 4 5 6 7 8 1 / \ 2 2 / \ 3 3 / \ 4 4 false
方法一、后序遍历 + 剪枝 (从底至顶)
思路是对二叉树做后序遍历,从底至顶返回子树深度,若判定某子树不是平衡树则 “剪枝” ,直接向上返回。
算法流程:
recur(root) 函数:
返回值:
1 2 3 当节点root 左 / 右子树的深度差 \leq 1≤1 :则返回当前子树的深度,即节点 root 的左 / 右子树的深度最大值 +1+1 ( max(left, right) + 1 ); 当节点root 左 / 右子树的深度差 > 2>2 :则返回 -1−1 ,代表 此子树不是平衡树 。
终止条件:
1 2 3 4 当 root 为空:说明越过叶节点,因此返回高度 0 ; 当左(右)子树深度为 -1 :代表此树的 左(右)子树 不是平衡树,因此剪枝,直接返回 -1 ; isBalanced(root) 函数:
返回值:
1 若 recur(root) != -1 ,则说明此树平衡,返回 true ; 否则返回 false 。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public boolean isBalanced (TreeNode root) { return recur(root) != -1 ; } int recur (TreeNode root) { if (root == null )return 0 ; int left = recur(root.left); if (left == -1 )return -1 ; int right = recur(root.right); if (right == -1 )return -1 ; return Math.abs(left - right) < 2 ? Math.max(left,right)+1 :-1 ; } }
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
1 2 3 4 5 输入: n = 3 输出: 6 输入: n = 9 输出: 45
方法一、递归
时间复杂度:O(n)
空间复杂度:O(n)
代码
1 2 3 4 5 6 class Solution { public int sumNums (int n) { boolean flag = n >0 && (n+=sumNums(n-1 )) >0 ; return n; } }
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
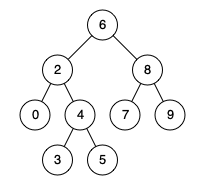
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
1 2 3 4 5 6 7 8 9 10 11 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。 所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。
方法一:迭代
循环搜索: 当节点 rootroot 为空时跳出;
当 p, qp,q 都在 rootroot 的 右子树 中,则遍历至 root.rightroot.right ;
否则,当 p, qp,q 都在 rootroot 的 左子树 中,则遍历至 root.leftroot.left ;
否则,说明找到了 最近公共祖先 ,跳出。
时间复杂度 O(N)O(N) : 其中 NN 为二叉树节点数;每循环一轮排除一层,二叉搜索树的层数最小为 \log NlogN (满二叉树),最大为 NN (退化为链表)。
空间复杂度 O(1)O(1) : 使用常数大小的额外空间。
递归代码
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { while (root!=null ){ if (root.val > p.val && root.val > q.val)root = root.left; else if (root.val < p.val && root.val < q.val)root = root.right; else break ; } return root; } }
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
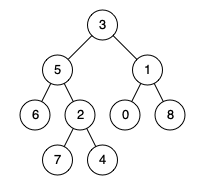
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
1 2 3 4 5 6 7 8 9 10 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。 所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉树中。
pp 和 qq 在 rootroot 的子树中,且分列 rootroot 的 异侧(即分别在左、右子树中);
p = rootp=root ,且 qq 在 rootroot 的左或右子树中;
q = rootq=root ,且 pp 在 rootroot 的左或右子树中;
递归解析:
终止条件:
1 当越过叶节点,则直接返回 nullnull ;当 rootroot 等于 p, qp,q ,则直接返回 rootroot ;
递推工作:
1 2 开启递归左子节点,返回值记为 leftleft ; 开启递归右子节点,返回值记为 rightright ;
返回值:
根据 leftleft 和 rightright ,可展开为四种情况;
1 2 3 4 5 6 7 8 9 当 leftleft 和 rightright 同时为空 :说明 rootroot 的左 / 右子树中都不包含 p,qp,q ,返回 nullnull ; 当 leftleft 和 rightright 同时不为空 :说明 p, qp,q 分列在 rootroot 的 异侧 (分别在 左 / 右子树),因此 rootroot 为最近公共祖先,返回 rootroot ; 当 leftleft 为空 ,rightright 不为空 :p,qp,q 都不在 rootroot 的左子树中,直接返回 rightright 。具体可分为两种情况: p,qp,q 其中一个在 rootroot 的 右子树 中,此时 rightright 指向 pp(假设为 pp ); p,qp,q 两节点都在 rootroot 的 右子树 中,此时的 rightright 指向 最近公共祖先节点 ; 当 leftleft 不为空 , rightright 为空 :与情况 3. 同理;
时间复杂度 O(N)O(N) : 其中 NN 为二叉树节点数;最差情况下,需要递归遍历树的所有节点。
空间复杂度 O(N)O(N) : 最差情况下,递归深度达到 NN ,系统使用 O(N)O(N) 大小的额外空间。
递归代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q)return root; TreeNode left = lowestCommonAncestor(root.left , p , q); TreeNode right = lowestCommonAncestor(root.right , p , q); if ( left == null && right == null ) return null ; if ( left == null ) return right; if ( right == null ) return left; return root; } }
11.排序(简单) 输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
1 2 3 4 5 6 7 8 9 输入: [10,2] 输出: "102" 输入: [3,30,34,5,9] 输出: "3033459" 0 < nums.length <= 100 输出结果可能非常大,所以你需要返回一个字符串而不是整数 拼接起来的数字可能会有前导 0,最后结果不需要去掉前导 0
方法一、
若拼接字符串 x + y > y + x,则 x “大于” y ;
反之,若 x + y < y + x,则 x “小于” y ;
时间复杂度 O(NlogN) : N 为最终返回值的字符数量( strs 列表的长度 ≤N );使用快排或内置函数的平均时间复杂度为 O(NlogN) ,最差为 O(N^2)
空间复杂度 O(N) : 字符串列表 strs 占用线性大小的额外空间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public String minNumber (int [] nums) { String[] str = new String [nums.length]; for (int i = 0 ; i < nums.length ; i++)str[i] = String.valueOf(nums[i]); Arrays.sort(str,(x,y)->(x+y).compareTo(y+x)); StringBuilder res = new StringBuilder (); for (String s : str){ res.append(s); } return res.toString(); } }
自己写快排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { public String minNumber (int [] nums) { String[] strs = new String [nums.length]; for (int i = 0 ; i < nums.length; i++) strs[i] = String.valueOf(nums[i]); quickSort(strs, 0 , strs.length - 1 ); StringBuilder res = new StringBuilder (); for (String s : strs) res.append(s); return res.toString(); } void quickSort (String[] strs, int l, int r) { if (l >= r) return ; int i = l, j = r; String tmp = strs[i]; while (i < j) { while ((strs[j] + strs[l]).compareTo(strs[l] + strs[j]) >= 0 && i < j) j--; while ((strs[i] + strs[l]).compareTo(strs[l] + strs[i]) <= 0 && i < j) i++; tmp = strs[i]; strs[i] = strs[j]; strs[j] = tmp; } strs[i] = strs[l]; strs[l] = tmp; quickSort(strs, l, i - 1 ); quickSort(strs, i + 1 , r); } }
从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
1 2 3 4 5 输入: [1,2,3,4,5] 输出: True 输入: [0,0,1,2,5] 输出: True
方法一: 集合 Set + 遍历
遍历五张牌,遇到大小王(即 0 )直接跳过。
判别重复: 利用 Set 实现遍历判重, Set 的查找方法的时间复杂度为 O(1) ;
获取最大 / 最小的牌: 借助辅助变量 mama 和 mimi ,遍历统计即可。
复杂度分析:
时间复杂度 O(N) = O(5) = O(1): 其中 NN 为 nums 长度,本题中 N \equiv 5N≡5 ;遍历数组使用 O(N) 时间。
空间复杂度 O(N) = O(5) = O(1): 用于判重的辅助 Set 使用 O(N) 额外空间。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public boolean isStraight (int [] nums) { int max=0 ,min=14 ; Set<Integer> set = new HashSet <>(); for (int i = 0 ; i < nums.length; i++){ if (nums[i] == 0 )continue ; max = Math.max(max,nums[i]); min = Math.min(min,nums[i]); if (set.contains(nums[i]))return false ; set.add(nums[i]); } return ( max - min ) < 5 ; } }
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
1 2 3 4 5 6 7 8 输入:arr = [3 ,2 ,1 ], k = 2 输出:[1 ,2 ] 或者 [2 ,1 ] 输入:arr = [0 ,1 ,2 ,1 ], k = 1 输出:[0 ] 0 <= k <= arr.length <= 10000 0 <= arr[i] <= 10000
方法一:排序
思路和算法
对原数组从小到大排序后取出前 k 个数即可。
复杂度分析
时间复杂度:O(nlogn),其中 nn 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂度。
空间复杂度:O(logn),排序所需额外的空间复杂度为 O(logn)。
方法一代码
1 2 3 4 5 6 7 8 9 10 class Solution { public int [] getLeastNumbers(int [] arr, int k) { int [] vec = new int [k]; Arrays.sort(arr); for (int i = 0 ; i < k; ++i) { vec[i] = arr[i]; } return vec; } }
方法二:堆
我们用一个大根堆实时维护数组的前 kk 小值。首先将前 kk 个数插入大根堆中,随后从第 k+1k+1 个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public int [] getLeastNumbers(int [] arr, int k) { int [] vec = new int [k]; if (k == 0 ) { return vec; } PriorityQueue<Integer> queue = new PriorityQueue <Integer>(new Comparator <Integer>() { public int compare (Integer num1, Integer num2) { return num2 - num1; } }); for (int i = 0 ; i < k; ++i) { queue.offer(arr[i]); } for (int i = k; i < arr.length; ++i) { if (queue.peek() > arr[i]) { queue.poll(); queue.offer(arr[i]); } } for (int i = 0 ; i < k; ++i) { vec[i] = queue.poll(); } return vec; } }
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
1 2 3 4 5 6 7 8 9 10 11 输入: ["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"] [[],[1],[2],[],[3],[]] 输出:[null,null,null,1.50000,null,2.00000] 输入: ["MedianFinder","addNum","findMedian","addNum","findMedian"] [[],[2],[],[3],[]] 输出:[null,null,2.00000,null,2.50000] 最多会对 addNum、findMedian 进行 50000 次调用。
方法一、堆
维护A,B两个堆,将数据大的一半放入B中,小的一半放入A中,去中位数从A,B顶端取出元素比较即可。
时间复杂度
1 2 查找中位数 O(1) : 获取堆顶元素使用 O(1) 时间; 添加数字 O(logN) : 堆的插入和弹出操作使用 O(logN) 时间。
空间复杂度O(N) :其中 N* 为数据流中的元素数量,小顶堆 A* 和大顶堆 B* 最多同时保存 N 个元素。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class MedianFinder { PriorityQueue<Integer> A,B; public MedianFinder () { A = new PriorityQueue <>(); B = new PriorityQueue <>( (x,y) -> (y-x) ); } public void addNum (int num) { if (A.size()!=B.size()){ A.add(num); B.add(A.poll()); }else { B.add(num); A.add(B.poll()); } } public double findMedian () { return A.size() == B.size() ? ( A.peek()+B.peek() )/2.0 : A.peek(); } }
分治算法(中等) 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
1 2 Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
1 2 3 4 Input: preorder = [-1], inorder = [-1] Output: [-1] 0 <= 节点个数 <= 5000
方法一:递归
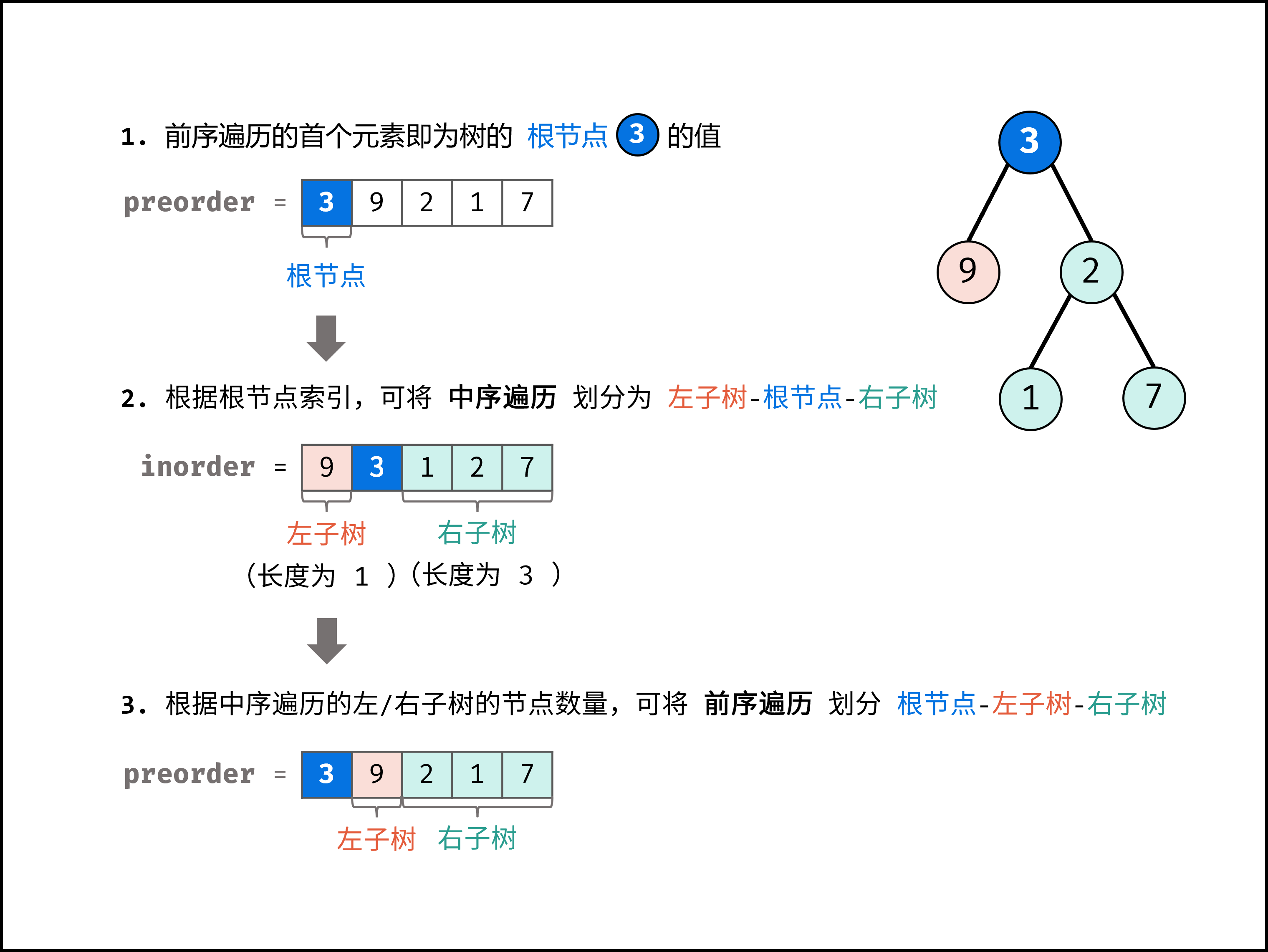
前序遍历性质: 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。
中序遍历性质: 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。
根据以上性质,可得出以下推论:
前序遍历的首元素 为 树的根节点 node 的值。
在中序遍历中搜索根节点 node 的索引 ,可将 中序遍历 划分为 [ 左子树 | 根节点 | 右子树 ] 。
根据中序遍历中的左(右)子树的节点数量,可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ]
通过以上三步,可确定 三个节点 :1.树的根节点、2.左子树根节点、3.右子树根节点。
根据「分治算法」思想,对于树的左、右子树,仍可复用以上方法划分子树的左右子树。
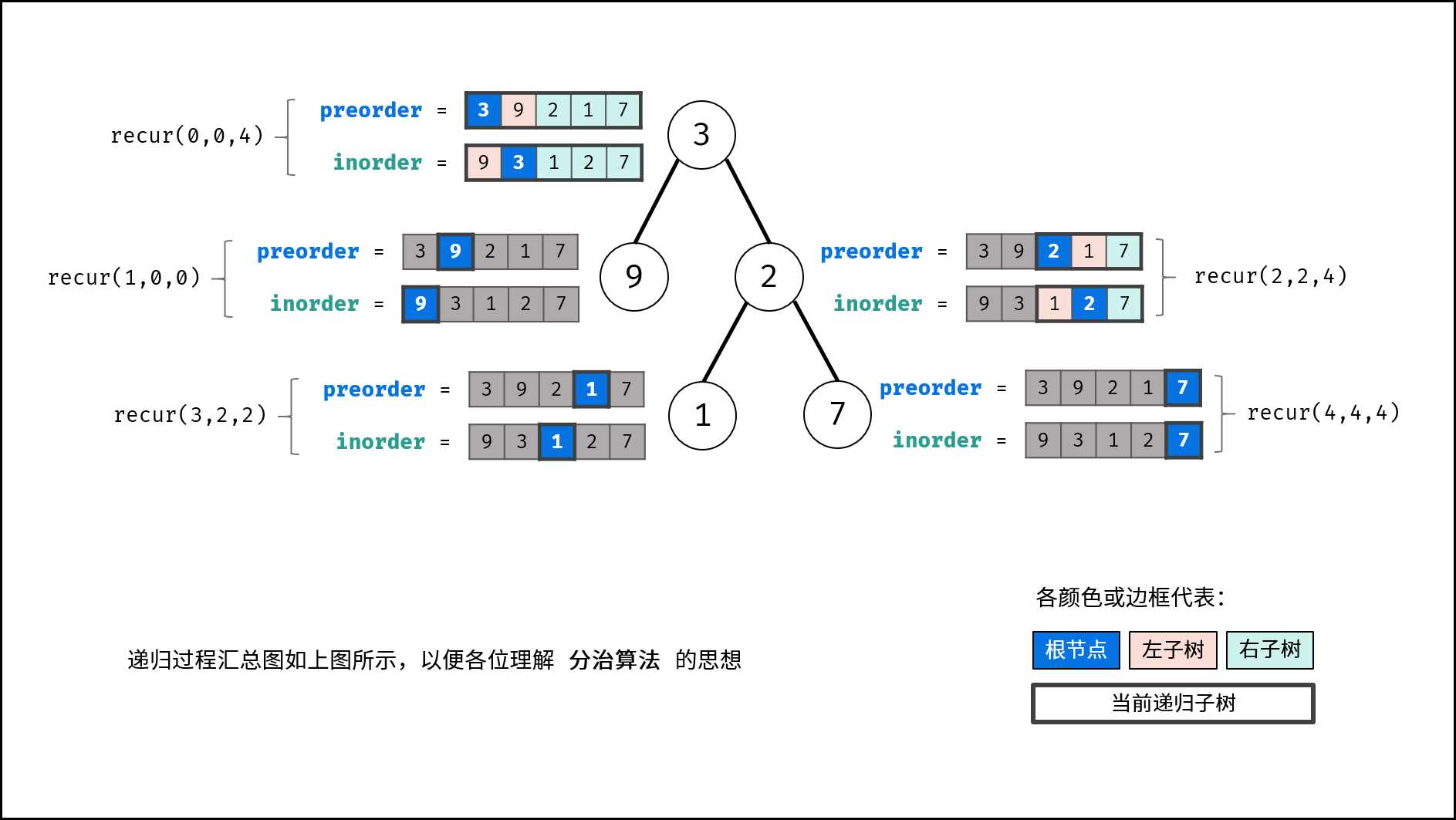
分治算法解析:
递推参数: 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ;
终止条件: 当 left > right ,代表已经越过叶节点,此时返回 nullnull ;
递推工作:
1.建立根节点 node : 节点值为 preorder[root] ;
2.划分左右子树: 查找根节点在中序遍历 inorder 中的索引 i ;
为了提升效率,本文使用哈希表 dic 存储中序遍历的值与索引的映射,查找操作的时间复杂度为 O(1)O(1) ;
3.构建左右子树: 开启左右子树递归;
根节点索引
中序遍历左边界
中序遍历右边界
左子树 root + 1left
右子树 i - left + root + 1i + 1
TIPS: i - left + root + 1含义为 根节点索引 + 左子树长度 + 1
时间复杂度 O(N)O(N) : 其中 NN 为树的节点数量。初始化 HashMap 需遍历 inorder ,占用 O(N)O(N) 。递归共建立 NN 个节点,每层递归中的节点建立、搜索操作占用 O(1)O(1) ,因此使用 O(N)O(N) 时间。
空间复杂度 O(N)O(N) : HashMap 使用 O(N)O(N) 额外空间;最差情况下(输入二叉树为链表时),递归深度达到 NN ,占用 O(N)O(N) 的栈帧空间;因此总共使用 O(N)O(N) 空间。
方法一、递归代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution { HashMap<Integer,Integer> inorderMap = new HashMap <>(); int [] preorderArry; public TreeNode buildTree (int [] preorder, int [] inorder) { for (int i = 0 ; i < inorder.length; i++){ inorderMap.put(inorder[i],i); } this .preorderArry = preorder; return recur(0 ,0 ,preorder.length-1 ); } TreeNode recur (int root, int left, int right) { if (left>right)return null ; TreeNode node = new TreeNode (preorderArry[root]); int i = inorderMap.get(preorderArry[root]); node.left = recur(root + 1 , left , i - 1 ); node.right = recur(root + 1 - left + i , i + 1 , right); return node; } }
实现 pow(x , n ) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。
1 2 3 4 5 6 7 8 9 输入:x = 2.00000, n = 10 输出:1024.00000 输入:x = 2.10000, n = 3 输出:9.26100 输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
快速幂解析(二进制角度):
注意 java中int类型是有符号的 ,负的下限 绝对这 比正的上限 绝对值大一 ,要切换成long型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public double myPow (double x, int n) { if (x == 0 ) return 0 ; long b = n; double res = 1.0 ; if (b < 0 ) { x = 1 / x; b = -b; } while (b > 0 ) { if ((b & 1 ) == 1 ) res *= x; x *= x; b >>= 1 ; } return res; } }
后序遍历定义: [ 左子树 | 右子树 | 根节点 ] ,即遍历顺序为 “左、右、根” 。
二叉搜索树定义: 左子树中所有节点的值 << 根节点的值**;**右子树中所有节点的值 >> 根节点的值 ;其左、右子树也分别为二叉搜索树。
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
示例 :
1 2 3 4 5 6 7 输入: [1,6,3,2,5] 输出: false 输入: [1,3,2,6,5] 输出: true 数组长度 <= 1000
方法一:递归分治
根据二叉搜索树的定义,可以通过递归,判断所有子树的 正确性 (即其后序遍历是否满足二叉搜索树的定义) ,若所有子树都正确,则此序列为二叉搜索树的后序遍历。
递归解析:
终止条件: 当 i≥j ,说明此子树节点数量 ≤1 ,无需判别正确性,因此直接返回 truetrue ;
递推工作:
1.划分左右子树: 遍历后序遍历的 [i, j][i,j] 区间元素,寻找 第一个大于根节点 的节点,索引记为 m 。此时,可划分出左子树区间 [i,m-1][i,m−1] 、右子树区间 [m, j - 1][m,j−1] 、根节点索引 j 。
2.判断是否为二叉搜索树:
1 2 3 1.左子树区间 [i, m - 1][i,m−1] 内的所有节点都应 << postorder[j]postorder[j] 。而第 1.划分左右子树 步骤已经保证左子树区间的正确性,因此只需要判断右子树区间即可。 2.右子树区间 [m, j-1][m,j−1] 内的所有节点都应 >> postorder[j]postorder[j] 。实现方式为遍历,当遇到 \leq postorder[j]≤postorder[j] 的节点则跳出;则可通过 p = jp=j 判断是否为二叉搜索树。
返回值: 所有子树都需正确才可判定正确,因此使用 与逻辑符 &&& 连接。
1 2 3 1.p = jp=j : 判断 此树 是否正确。 2.recur(i, m - 1)recur(i,m−1) : 判断 此树的左子树 是否正确。 3.recur(m, j - 1)recur(m,j−1) : 判断 此树的右子树 是否正确。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public boolean verifyPostorder (int [] postorder) { return recur(postorder, 0 , postorder.length-1 ); } boolean recur (int [] postorder, int i, int j) { if (i>=j)return true ; int p = i; while (postorder[p]<postorder[j])p++; int m = p; while (postorder[p]>postorder[j])p++; return p = = j && recur(postorder,i,m-1 ) && recur(postorder,m,j-1 ); } }
位运算(简单) 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为 汉明重量 ).)。
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
1 2 3 4 5 6 7 8 9 10 11 12 13 输入:n = 11 (控制台输入 00000000000000000000000000001011) 输出:3 解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。 输入:n = 128 (控制台输入 00000000000000000000000010000000) 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。 输入:n = 4294967293 (控制台输入 11111111111111111111111111111101,部分语言中 n = -3) 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。 输入必须是长度为 32 的 二进制串 。
方法一、循环检查二进制位
1 2 3 4 5 6 7 8 9 10 11 public class Solution { public int hammingWeight (int n) { int cnt = 0 ; while (n!=0 ){ if ( (n & 1 ) == 1 )cnt++; n >>>= 1 ; } return cnt; } }
方法二:位运算优化
1 n & (n−1)其预算结果恰为把 n 的二进制位中的最低位的 1 变为 0 之后的结果。
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
1 2 3 4 5 输入: a = 1, b = 1 输出: 2 a, b 均可能是负数或 0 结果不会溢出 32 位整数
方法一、位运算
在计算机系统中,数值一律用 补码 来表示和存储。补码的优势: 加法、减法可以统一处理(CPU只有加法器)。因此,以上方法 同时适用于正数和负数的加法 。
1 2 3 4 5 6 7 8 9 10 class Solution { public int add (int a, int b) { while (b!=0 ){ int c = a ^ b; b = (a & b)<<1 ; a = c; } return a ; } }
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
1 2 3 4 5 6 7 输入:nums = [4,1,4,6] 输出:[1,6] 或 [6,1] 输入:nums = [1,2,10,4,1,4,3,3] 输出:[2,10] 或 [10,2] 2 <= nums.length <= 10000
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int [] singleNumbers(int [] nums) { int res = 0 ; for (int i = 0 ; i < nums.length ; i++){ res ^= nums[i]; } int b = 1 ; while ( (res & b) == 0 )b <<= 1 ; int resultA = 0 , resultB = 0 ; for (int i = 0 ; i < nums.length ; i++){ if ((nums[i] & b) != 0 ) resultA ^= nums[i]; else resultB ^= nums[i]; } return new int [] {resultA,resultB}; } }
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
1 2 3 4 5 6 7 8 9 输入:nums = [3,4,3,3] 输出:4 输入:nums = [9,1,7,9,7,9,7] 输出:1 限制: 1 <= nums.length <= 10000 1 <= nums[i] < 2^31
统计每一个出现的次数
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int singleNumber (int [] nums) { int [] sumBitCount = new int [32 ]; for (int i = 0 ; i < nums.length ; i++){ int b = 1 ; for (int j = 0 ; j < 32 ; j++ ){ sumBitCount[j] += ((nums[i] & b) != 0 ? 1 : 0 ); b <<= 1 ; } } int rec = 0 ; for (int i = 0 ; i < 32 ; i++){ rec |= ( (sumBitCount[i] % 3 ) & 1 ) << i; } return rec; } }
数学(简单) 数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
1 2 3 4 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2 1 <= 数组长度 <= 50000
方法一、哈希表
每个数次出现的次数,如果最大出现次数大于数组一半,直接返回
时间复杂度:O(N)
空间复杂度:O(N)
方法二、中位数法
排序一下,取中位数
时间复杂度:O(nlogn)
空间复杂度:O(nlogn)
方法三、Boyer-Moore 投票算法
既然是大于数组一般,直接让该数出现一次+1, 出现别的-1; =0 时换数字, 最终和一定大于0
时间复杂度:O(n)
空间复杂度:O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public int majorityElement (int [] nums) { int count = 0 ; int candidate = 0 ; for (int i = 0 ; i < nums.length ; i++){ if (count == 0 ){ candidate = nums[i]; } count += nums[i] == candidate ? 1 : -1 ; } return candidate; } }
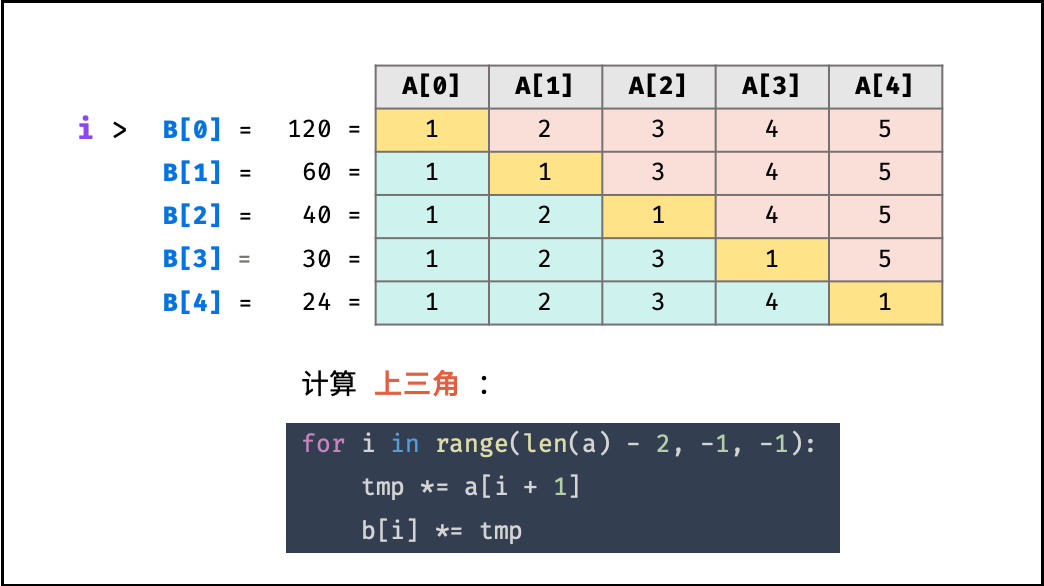
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
1 2 3 4 5 输入: [1,2,3,4,5] 输出: [120,60,40,30,24] 所有元素乘积之和不会溢出 32 位整数 a.length <= 100000
根据表格的主对角线(全为 11 ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
时间复杂度:O(n)
空间复杂度:O(1)
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int [] constructArr(int [] a) { int leng = a.length; if (leng == 0 )return new int [0 ]; int [] b = new int [leng]; b[0 ] = 1 ; for (int i = 1 ; i <leng ; i++ ){ b[i] = b[i-1 ]*a[i-1 ]; } int tem = 1 ; for (int i = leng-2 ; i >=0 ; i-- ){ tem *= a[i+1 ]; b[i] *= tem; } return b; } }
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1] …*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
1 2 3 4 5 6 7 输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1 输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
方法一、数学法
1 2 3 4 5 6 7 8 9 class Solution { public int cuttingRope (int n) { if (n <= 3 ) return n - 1 ; int a = n / 3 , b = n % 3 ; if (b == 0 ) return (int )Math.pow(3 , a); if (b == 1 ) return (int )Math.pow(3 , a - 1 ) * 4 ; return (int )Math.pow(3 , a) * 2 ; } }
方法二、通用法 贪心
和方法一一样,通过N=1,2,3,4,5,6 …找到规律
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
1 2 3 4 5 6 7 输入:target = 9 输出:[[2,3,4],[4,5]] 输入:target = 15 输出:[[1,2,3,4,5],[4,5,6],[7,8]] 1 <= target <= 10^5
方法一、枚举+暴力
方法一、枚举+数学优化
根据连续数,首项加末项×项数除以2 = target
(x+y)×(y−x+1)/2 = target ,变成 y 2+y −x 2+x −2×target =0
a =1,b =1,c =−x 2+x −2×target 直接用求根公式
判别式 b^2-4ac 开根需要为整数
最后的求根公式的分子需要为偶数,因为分母为 2
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public int [][] findContinuousSequence(int target) { List<int []> vec = new ArrayList <int []>(); int sum = 0 , limit = (target - 1 ) / 2 ; for (int x = 1 ; x <= limit; ++x) { long delta = 1 - 4 * (x - (long ) x * x - 2 * target); if (delta < 0 ) { continue ; } int delta_sqrt = (int ) Math.sqrt(delta + 0.5 ); if ((long ) delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1 ) % 2 == 0 ) { int y = (-1 + delta_sqrt) / 2 ; if (x < y) { int [] res = new int [y - x + 1 ]; for (int i = x; i <= y; ++i) { res[i - x] = i; } vec.add(res); } } } return vec.toArray(new int [vec.size()][]); } }
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
1 2 3 4 5 6 7 8 输入: n = 5, m = 3 输出: 3 输入: n = 10, m = 17 输出: 2 1 <= n <= 10^5 1 <= m <= 10^6
方法一:数学 + 递归
时间复杂度:O (n ),需要求解的函数值有 n 个。
空间复杂度:O (n ),函数的递归深度为 n,需要使用 O (n) 的栈空间。
1 2 3 4 5 一个人的时候: 这个活着的人的下标是0. 所以需要知道当两个人存在的时候,这个人的下标是多少; 两个人的时候: 这个活着的人下标:(0+3)%2=1 所以需要知道当三个人存在的时候 ,这个人的下标是多少; 三个人的时候: 这个活着的人下标:(1+3)%3=1 所以需要知道当四个人存在的时候 ,这个人的下标是多少;
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int lastRemaining (int n, int m) { return f(n, m); } public int f (int n, int m) { if (n == 1 ) { return 0 ; } int x = f(n - 1 , m); return (m + x) % n; } }
方法二:数学 + 迭代
时间复杂度:O(n),需要求解的函数值有 n 个。
空间复杂度:O(1),只使用常数个变量。
1 2 3 4 5 6 7 8 9 class Solution { public int lastRemaining (int n, int m) { int f = 0 ; for (int i = 2 ; i != n + 1 ; ++i) { f = (m + f) % i; } return f; } }
模拟(中等) 输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
1 2 3 4 5 6 7 8 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5] 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7] 0 <= matrix.length <= 100 0 <= matrix[i].length <= 100
矩阵 左、右、上、下 四个边界 l , r , t , b ,用于打印的结果列表 res 。
1 2 3 时间复杂度 O(MN): M, NM,N 分别为矩阵行数和列数。 空间复杂度 O(1) : 四个边界 l , r , t , b 使用常数大小的 额外 空间( res 为必须使用的空间)。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public int [] spiralOrder(int [][] matrix) { if (matrix == null ||matrix.length == 0 )return new int [0 ]; int l = 0 , r = matrix[0 ].length - 1 , t = 0 , b = matrix.length - 1 ; int [] res = new int [ (b+1 )*(r+1 ) ]; int x = 0 ; while (true ){ for (int i = l; i <= r ; i++)res[x++] = matrix[t][i]; if (t++ >= b)break ; for (int i = t; i <= b ; i++)res[x++] = matrix[i][r]; if (r-- <= l)break ; for (int i = r; i >= l ; i--)res[x++] = matrix[b][i]; if (b-- <= t)break ; for (int i = b; i >= t ; i--)res[x++] = matrix[i][l]; if (l++ >= r)break ; } return res; } }
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
1 2 3 4 5 6 7 8 9 10 11 12 13 输入:pushed = [1 ,2 ,3 ,4 ,5 ], popped = [4 ,5 ,3 ,2 ,1 ] 输出:true 解释:我们可以按以下顺序执行: push(1 ), push(2 ), push(3 ), push(4 ), pop() -> 4 , push(5 ), pop() -> 5 , pop() -> 3 , pop() -> 2 , pop() -> 1 输入:pushed = [1 ,2 ,3 ,4 ,5 ], popped = [4 ,3 ,5 ,1 ,2 ] 输出:false 解释:1 不能在 2 之前弹出。 0 <= pushed.length == popped.length <= 1000 0 <= pushed[i], popped[i] < 1000 pushed 是 popped 的排列。
时间复杂度 O(N): 其中 NN 为列表 pushed 的长度;每个元素最多入栈与出栈一次,即最多共 2N 次出入栈操作。
空间复杂度 O(N): 辅助栈 stack 最多同时存储 N 个元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public boolean validateStackSequences (int [] pushed, int [] popped) { Stack<Integer> stack = new Stack <>(); int i = 0 ; for (int nums : pushed){ stack.push(nums); while (!stack.isEmpty() && stack.peek() == popped[i]){ stack.pop(); i++; } } return stack.isEmpty(); } }
字符串(中等) 请实现一个函数用来判断字符串是否表示数值 (包括整数和小数)。
数值 (按顺序)可以分成以下几个部分:
若干空格
一个 小数 或者 整数
(可选)一个 'e' 或 'E' ,后面跟着一个 整数
若干空格
小数(按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
下述格式之一:
至少一位数字,后面跟着一个点 '.'
至少一位数字,后面跟着一个点 '.' ,后面再跟着至少一位数字
一个点 '.' ,后面跟着至少一位数字
整数 (按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
至少一位数字
部分数值 列举如下:
1 ["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]
部分非数值 列举如下:
1 ["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 输入:s = "0" 输出:true 输入:s = "e" 输出:false 输入:s = "." 输出:false 输入:s = " .1 " 输出:true 1 <= s.length <= 20 s 仅含英文字母(大写和小写),数字(0-9),加号 '+' ,减号 '-' ,空格 ' ' 或者点 '.' 。
二、力扣热题 HOT 100 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
1 2 3 4 5 6 7 8 9 输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。 输入:nums = [3,2,4], target = 6 输出:[1,2] 输入:nums = [3,3], target = 6 输出:[0,1]
解题思路:
1.暴力穷举
2.利用哈希表,每次查找一下当前值和哈希表是否重复,不重复存储target-当前值和下标值
代码
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int[] twoSum(int[] nums, int target) { Map<Integer,Integer> map = new HashMap<Integer,Integer>(); for(int i=0;i<nums.length;i++){ if(map.containsKey(target-nums[i])){ return new int[]{map.get(target-nums[i]),i}; } map.put(nums[i],i); } return new int[0]; } }